Category Theory
Zulip Server
Archive

You're reading the public-facing archive of the Category Theory Zulip server.
To join the server you need an invite. Anybody can get an invite by contacting Matteo Capucci at name dot surname at gmail dot com.
For all things related to this archive refer to the same person.

Stream: learning: questions

Topic: Euler and Venn diagrams

Keith Elliott Peterson (Sep 20 2021 at 00:07):

It is well known that Euler and Venn diagrams can be used to represent sets and relations of sets, however a while back I was watching a conference talk given by Vlad Patryshev on ITT and near the end, Vlad gives diagrams for the Sierpinski topos.

Video.

This has been itching at the back of my mind for a while: but for which categories can any object or relations of objects be represented as Euler/Venn diagrams?

For instance, $\mathrm{Set}$ obviously has such diagrams, and as Patryshev has shown in the video $\mathrm{Set}^\rightarrow$ does as well.

It should also be the case that for discrete categories $X$, the presheaf category $\mathrm{Set}^X$, ought to have $X$-indexed diagrams, with $\mathrm{Set}$ being the special case having only singleton-indexed diagrams.

Likewise, since the arrow category is a total order, extending the argument Patryshev gave, for any total order $(T,<)$, $\mathrm{Set}^{(T,<)}$ ought to have such (nested) diagrams as well.

So then, does every topos come with a generalization of Euler and Venn diagrams?

Pointed sets also have Euler snd Venn diagrams, where such diagrams come with a chosen basepoint. Does every category with a subobject classifier come a generalization of Euler/Venn diagrams?

And lastly, since such diagrammatics can be used as a learning, teaching, and proving aids; is there a systematic way to find and draw such representations, if and when they exist?

Morgan Rogers (he/him) (Sep 20 2021 at 07:32):

It's not too hard to imagine toposes, even presheaf toposes, which are too complex to admit such diagrams. Take a large enough total order, one of size $2^{\mathbb{R}}$ for instance, and the Euler-diagrammatic representation of presheaves on it will fail to literally capture the operations one might apply to subobjects because there aren't enough points in the plane. But that doesn't matter so much, because you can still get intuition from them... How precise of a statement are you after?

Keith Elliott Peterson (Sep 20 2021 at 20:30):

Morgan Rogers (he/him) said:

Take a large enough total order, one of size $2^{\mathbb{R}}$ for instance, and the Euler-diagrammatic representation of presheaves on it will fail to literally capture the operations one might apply to subobjects because there aren't enough points in the plane.

That's a good point I overlooked.

Morgan Rogers (he/him) said:

But that doesn't matter so much, because you can still get intuition from them... How precise of a statement are you after?

Okay fair enough. However, as categories, total orders are rather simple. Does that intuition still hold for non-total preorders and partial orders; and other categories in general?

If possible, I wouldn't mind statements precise enough I could program a computer to give such drawings, assuming I'm not being too ambitious.

Morgan Rogers (he/him) (Sep 21 2021 at 07:30):

There is a nice representation theorem that says that any distributive lattice can be embedded into a "field of sets", which is to say that it can be embedded into a powerset lattice. Powerset lattices are manifestly what standard Venn diagrams represent, so I wouldn't be surprised if any distributive lattice (or any poset which embeds into a distributive lattice, which might be... all of them?) can be represented by an Euler diagram. However, the problem is more of finding such a representation which is flexible enough to visually (at least in theory) illustrate the subobject operations which you liked in Patryshev's video, which I think will impose some constraints on shape somehow.

Morgan Rogers (he/him) (Sep 21 2021 at 07:31):

Note that circles and even ellipses produce messy Venn diagrams when we get to 5 or more! It's amusing to look at and think about the shapes that people have come up with for higher numbers on the Wikipedia page

Jens Hemelaer (Sep 21 2021 at 09:18):

You can also think about categories $\mathcal{C}$ that admit a functor
$F : \mathcal{C} \to \mathbf{Set}$
such that $F$ is faithful and conservative and such that $F$ preserves monomorphisms.

Then each object $X$ of $\mathcal{C}$ can be thought of as a "set with extra structure" $F(X)$, and different subobjects of $X$ correspond to different subsets of $F(X)$.

Many categories admit such a functor $F$, for example small categories, Grothendieck toposes, or categories of algebraic structures (rings, groups, lattices,...).

Keith Elliott Peterson (Sep 21 2021 at 23:00):

Morgan Rogers (he/him) said:

There is a nice representation theorem that says that any distributive lattice can be embedded into a "field of sets", which is to say that it can be embedded into a powerset lattice. Powerset lattices are manifestly what standard Venn diagrams represent, so I wouldn't be surprised if any distributive lattice (or any poset which embeds into a distributive lattice, which might be... all of them?) can be represented by an Euler diagram.

It sounds like you're speaking about the down set construction; if memory serves me, is the Yoneda embedding for (0,1)-categories.

Morgan Rogers (he/him) said:

However, the problem is more of finding such a representation which is flexible enough to visually (at least in theory) illustrate the subobject operations which you liked in Patryshev's video, which I think will impose some constraints on shape somehow.

Wouldn't it just be a matter of finding how various simple categories of presheaves have subobjects represented as Euler and Venn diagrams and generalizing from there? For instance, $\mathrm{Set}^\rightarrow$ tells us what arrows in $C$ 'ought' to look like in $[C,\mathrm{Set}]$. Though really, my gut tells me these diagrams are actually defined by a universal property of subobject classifiers.

Morgan Rogers (he/him) (Sep 22 2021 at 07:25):

Keith Peterson said:

For instance, $\mathrm{Set}^\rightarrow$ tells us what arrows in $C$ 'ought' to look like in $[C,\mathrm{Set}]$. Though really, my gut tells me these diagrams are actually defined by a universal property of subobject classifiers.

I don't really understand this comment. For example, what should a Venn diagram for the double arrow category $A \rightrightarrows B$ look like?

Keith Elliott Peterson (Sep 22 2021 at 16:45):

Morgan Rogers (he/him) said:

Keith Peterson said:

For instance, $\mathrm{Set}^\rightarrow$ tells us what arrows in $C$ 'ought' to look like in $[C,\mathrm{Set}]$. Though really, my gut tells me these diagrams are actually defined by a universal property of subobject classifiers.

I don't really understand this comment. For example, what should a Venn diagram for the double arrow category $A \rightrightarrows B$ look like?

Do double arrow categories come with subobject classifiers?

Morgan Rogers (he/him) (Sep 22 2021 at 17:04):

I mean you were asking about toposes, so if I take presheaves on that double arrow category, how would you represent a presheaf as a Venn diagram?

Keith Elliott Peterson (Sep 22 2021 at 17:51):

Morgan Rogers (he/him) said:

I mean you were asking about toposes, so if I take presheaves on that double arrow category, how would you represent a presheaf as a Venn diagram?

That's what I'm curious and asking about. That, and diagrams of presheaves on the walking span, the walking cospan, and the walking commuting square.

Morgan Rogers (he/him) (Sep 22 2021 at 18:07):

Okay, instead of asking the question, I'll say that I think you can probably make it work for most if not all posets (your walking span and cospan will be represented by the ordinary Venn diagram with two regions and "two disjoint disks contained in a larger disk", for example) but there's no immediate way to represent parallel arrows in one of these; you'll need to expand the framework to enable that. One way to do this is to add a dimension or two: the objects of your indexing category will be disks, while the morphisms will be mapping cylinders (oriented along a preferred axis perpendicular to the disks). The Venn diagram is what you get in the poset case when you can flatten everything down into the plane.

Keith Elliott Peterson (Sep 24 2021 at 23:46):

Morgan Rogers (he/him) said:

(your walking span and cospan will be represented by the ordinary Venn diagram with two regions and "two disjoint disks contained in a larger disk", for example)

That gives diagrams for presheaves of the walking cospan, but certainly, diagrams for presheaves of the walking span will be in some sense dual to .

Morgan Rogers (he/him) said:

but there's no immediate way to represent parallel arrows in one of these; you'll need to expand the framework to enable that. One way to do this is to add a dimension or two: the objects of your indexing category will be disks, while the morphisms will be mapping cylinders (oriented along a preferred axis perpendicular to the disks). The Venn diagram is what you get in the poset case when you can flatten everything down into the plane.

Why do you say that? Working through the similar reasoning Vlad did, the category of Quivers, $\mathrm{Set}^{\rightrightarrows^{op}}$, has representable functors $\rightrightarrows(-,0)$, and $\rightrightarrows(-,1)$.

Where,

$$\rightrightarrows(-,0)\cong \{\bullet \},$$

giving subobjects $\varnothing_0$ and $\bullet$. Therefore Euler/Venn diagrams of '$0$-figures' are equivalent to the diagrams in $\mathrm{Set}$, and we can safely ignore them (as Vlad seems to have done for $1$-figures of the copresheaf category $\mathrm{Set}^\rightarrow$).

For $\rightrightarrows(-,1)$,

$$\rightrightarrows(-,1)\cong (s \stackrel{e}{\to} t)$$

with subobjects $\varnothing_1$, $s$, $t$, $(s,t)$, and $(s \stackrel{e}{\to} t)$. Assuming these correspond to regions within the diagrams, then I give this as my attempt:
https://i.ibb.co/0jQc70z/image.png

Morgan Rogers (he/him) (Sep 25 2021 at 10:47):

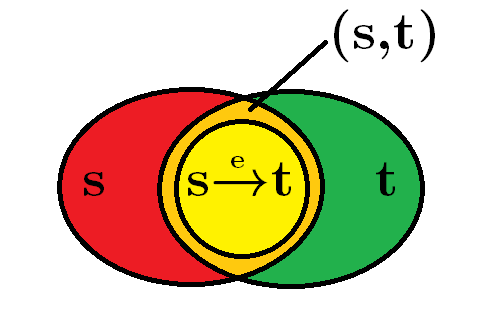
I should say something about Vlad's presentation that perhaps is leading to confusion here, or that perhaps would be clearer if I watched the rest of the video; I suspect this may be the case because I have no idea what you mean by '0-figures' and '1-figures'. The examples of subobjects he gives before introducing the Euler diagrams for $\mathrm{Set}^{\rightarrow}$ are subobjects of the terminal object. He also mentions the "point and a half". In all of these examples, the "tomorrow" value contains the "today" value as a subset. But this is not true for a general object of $\mathrm{Set}^{\rightarrow}$, so I've been interpreting the Euler diagrams heuristically: the outer circle represents "tomorrow" and the fact that the inner circle is contained in it is representing the fact that everything that exists "today" becomes something tomorrow; that there is a mapping involved, but that mapping need not be injective. For the subobject operations, we have ambient "today/always" and "tomorrow" sets, of which the subobjects pick out compatible subsets (hence the "never" region in those slides, representing the stuff that doesn't feature in either).

If that understanding is correct, then the problem I was pointing to is that this doesn't carry across to any category of presheaves containing parallel arrows, because there is no direct way to take shapes representing the values at the objects arranged in such a way as to represent multiple functions between those sets.

That said, your attempt seems promising. A problem I can see is that it only works for quivers where 'source' nodes aren't also 'target' nodes, and I can' see how you can combine them into a ingle region representing nodes without encountering the notational problem I was getting at above.